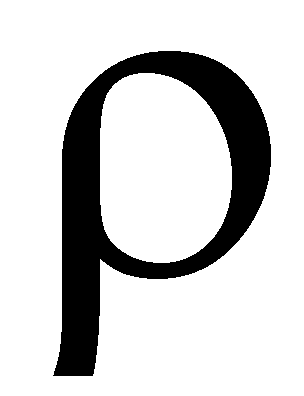Greeks are various functions that show the sensitivity of Fair Value of an option to changes in attributes related to the underlying and other market conditions. Greeks are a collection of statistical values that give the investor a better overall view of how a stock has been performing. These statistical values can be helpful in deciding what options strategies are best to use. The investor should remember that statistics show trends based on past performance. It is not guaranteed that the future performance of the stock will behave according to the historical numbers. These trends can change drastically based on new stock performance. The Greeks include Delta, Gamma, Vega, Theta, and Rho.
Delta
Delta is the change in the value of the option with respect to the change in the underlying asset price. Stated another way, it indicates the sensitivity of the option value to small changes in the underlying asset price.
For example, if the price of the underlying asset goes up by Rs.1.00 and the price of a call option on that asset goes up by Rs. 0.50, then the Delta of that option is said to be 0.50. So the option is moving half as fast as the asset at these levels. To make it clearer we can take Satyam as a case and see what is the effect of Greeks option on the price of its premium.
Suppose the Delta of an option of Satyam is 0.50 then every Rs.1.00 change in the price Satyam will make the value of the premium increase or decrease by Rs.0.50.
For example if the current price of Yes Bank is Rs.775 and the call option at the strike 780 is trading at a premium of Rs.14 with a Delta of 0.50, then every Rs.1.00 increase or decreases in the price of Satyam, will lead to increase or decreases in the premium amount by Rs.0.50.
If Delta is 1.00, then the move in the option price would be as large as the move in the asset price. But remember that you paid MUCH less for the option than you would for the asset. So your ROI (return-on-investment) is much more magnified than if you had purchased the underlying asset itself.
Call deltas are positive ranging from 0 to 1; put deltas are negative – ranging from -1 to 0.
At expiration, delta will approach 1 if the option is in-the-money; delta will approach 0 if the option is out-of-the-money.
If you are purchasing options to open a position, you would like to have a large delta. Then as the asset moves in the direction you predicted, you would reap high gains for a low investment. But you must trade this off against the price of the option. For example, Delta is higher for options that are deeper in-the-money, but they are more expensive. Frequently, a good trade-off is achieved by options that are at-the-money or slightly in-the-money.
Delta is also a very important parameter to consider when you are using options to hedge a position, so that you can correctly determine your mix of assets and options. Delta is also known as the hedge ratio.
Gamma
Delta is the rate of change of fair value of the option with respect to the change in the underlying asset price. However, Delta also changes as the asset price changes. Whereas Gamma another Greek parameters shows the sensitivity of the calculated Delta to small changes in the asset price. This parameter is called Gamma. Gamma is the rate of change of delta with respect to the underlying asset price. This parameter helps you to predict how delta will change as the asset price moves.
For example, a Gamma change of 0.150 indicates the Delta will increase or decrease by 0.150 if the underlying price increases or decreases by Rs1.00.
Taking the same example of Satyam, if Gamma of the Call option at strike 780 is 0.008 then with every Rs. 1.00 change in the price of Satyam, Delta of the Call option at strike 780 will change by 0.008.
At-the-money options have the highest Gammas. Gamma decreases as you go in-the-money or out-of-the-money. Gamma is sometimes used as a risk management tool to manage a large portfolio, because it tends to reflect the speed of the change in the option price. Options with high gamma are the most responsive to price movements, so they provide the most help in covering directional exposure.
Vega
Vega indicates the sensitivity of fair value of the option to small changes in the implied volatility. For ease of use, it is often expressed as the amount the option price would change with a one-percentage point increase in volatility.
For example, a Vega of 0.090 indicates that option’s theoretical value will increase by 0.090 if the volatility percentage is increased by 1.0 or decreased by .090 if the volatility percentage is decreased by 1.0.
For Example, if the Vega of Call option of Yes Bank at strike 780 is 0.384 then with every 1% increase or decrease change in Volatility will change the option theoretical price by Rs 0.384.
Vega is useful because volatility is one of the most important parameters determining the price of an option. Looking at historical volatility of the underlying asset price, implied volatility of the option price, and Vega can help you determine which options are likely to yield the best rewards for you.
When an asset has very high volatility – be sure to look closely at Vega. If you ignore this variable, you can be right about the asset moving significantly higher, yet the option you hold on that asset may move significantly lower due to a significant decrease in implied volatility.
Changes in volatility have a greater impact on options that are at-the-money, with a few months until expiration. The effect is less for options that are very close to expiration or very far from expiration. The effect is also less if the option is considerably in-the-money or out-of-the-money.
Theta
Theta indicates the sensitivity of the fair value of the option to small changes in time to expiration. For ease of use, it is often expressed as the amount the option price would decay in one day. It is shown as a negative number because the option loses time value as time passes. For a buyer of the option, this decay works against them; for a seller of the option, it works in their favor. For example, a theta of -0.250 indicates the option’s theoretical value will change by -0.250 if the day to expiration is reduced by 1.
For example, if the Theta of Call option of Yes Bank at strike 780 is -0.443 then with each passing day the theoretical value of call option of Satyam will decrease by Rs. 0.443.
For people who are relatively new to options trading, this is a very important lesson to learn: options are a decaying asset. As you get closer to expiration, the level of decay accelerates. Many traders liquidate or rollover their long positions when there is less than one month until expiration.
Rho
Rho indicates the sensitivity of the fair value of the option to small changes in the interest rate. For ease of use, it is often expressed as the amount the option price would change with a one-percentage point move in the interest rate. This parameter generally does not have as large an impact as the other Greeks. For example, a Rho of 0.060 indicates the option’s theoretical value will increase by Rs 0.060 if the interest rate is decreased by 1.0 % and Vice Versa.
For example if the Rho of Call option of Yes Bank at strike 780 is 0.115 then 1% change in interest rate will change.